f(x) = g(x) for all values of x...

Occasionally, you will get a problem that tells you that two expressions are equivalent for all values of some variable. Most often, these expressions are polynomials, and the variable used is x. What will often happen is that one or more coefficient on one side of the equation will be replaced by a letter or letters and you will be asked to find the value or possible values of one of those letters. These problems can be relatively simple to solve if you truly understand them.

Let's look at how these problems work using a series of images.  Apologies if these are slightly difficult to see.

In the image above, for the blue function, all of the coefficients are the same as the respective coefficients in the red function except for f, which is -49.

Here, we have a linear function with the equation y = -49.  All other blue coefficients are 0.  There is one point of overlap; thus, these functions are not equal for all values of x.

We now have a line that has a slope that is equivalent to the linear coefficient of the red function.

The final two coefficients of the blue function now match the final two coefficients of the red function.  All other blue coefficients are 0.  There are now two intersection points.

The final three coefficients are equivalent; we still only have two equivalent points.

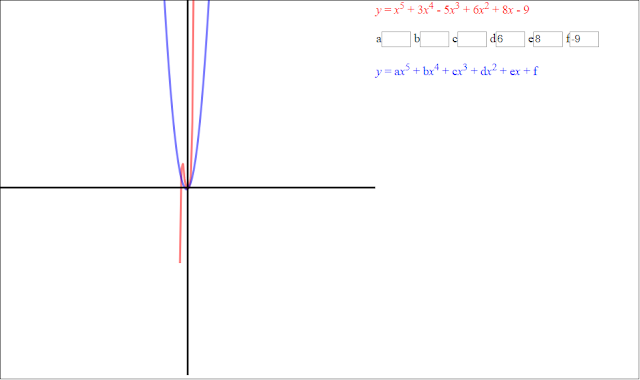
Now the last four coefficients are equivalent.  Parts of the left sides of the functions appear to be starting to line up, but there are still only two points of equivalency - when x = -3 and x = 0.

The only difference is now the first coefficient.  However, there is only one point of intersection - the y-intercept (0, -9).

Now that all of the coefficients are equivalent, we finally have a situation in which the functions are equivalent for all values of x.  Whenever you get a problem stating that two expressions are equivalent for all values of x, you must find the value of some missing coefficient that will make all corresponding coefficients on both sides of the equation equal.